哈希表

存储结构（冲突处理方式）

开放寻址法

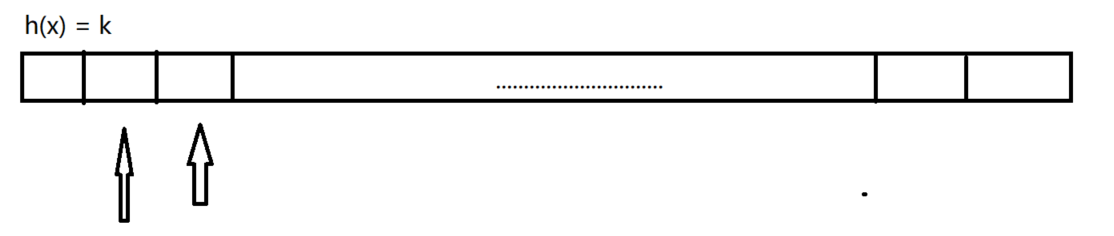
添加根据hash函数就算出对应的下标位置，然后再判断是否有冲突，有则继续判断下一个位置，直到无冲突为止。

查找查找操作与添加操作类似，也是相同的过程。

删除在hash表中并非直接删除，而是给删除的点打个标记，很少用。

模拟散列表

维护一个集合，支持如下几种操作：

I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；

现在要进行 N 次操作，对于每个询问操作输出对应的结果。

输入格式

第一行包含整数 N，表示操作数量。

接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式

对于每个询问指令 Q x，输出一个询问结果，如果 xx 在集合中出现过，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤N≤10e5 −10e9≤x≤10e9

输入样例：

输出样例：

1
2


Yes
No

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


# include <iostream>
# include <cstring>

using namespace std;

const int N = 200003, null = 0x3f3f3f3f; // 大于200000的最小质数

int h[N];

int find(int x)
{
	int k = (x % N + N) % N;
	
	while(h[k] != null && h[k] != x)
	{
		k++;
		if(k == N) k  = 0; // k走到最后一个位置就从头开始继续循环（空间开的很大，一般循环次数不多，不会死循环，开位置的时候开的都是数据的两倍，完全是用空间换时间。）
	}
	return k;
}

int main()
{
	int n;
	scanf("%d", &n);
	
	// 把所有的槽先清空(单链表-1表示空指针)
	memset(h, 0x3f, sizeof(h)); 
	
	while(n --)
	{
		char op[2];
		int x;
		scanf("%s%d", op, &x)；
		
		int k = find(x);
		if(*op == 'I') h[k] = x;
		else 
		{
			if(h[k] != null) puts("YES");
			else puts("NO");
		}
	}
}

拉链法

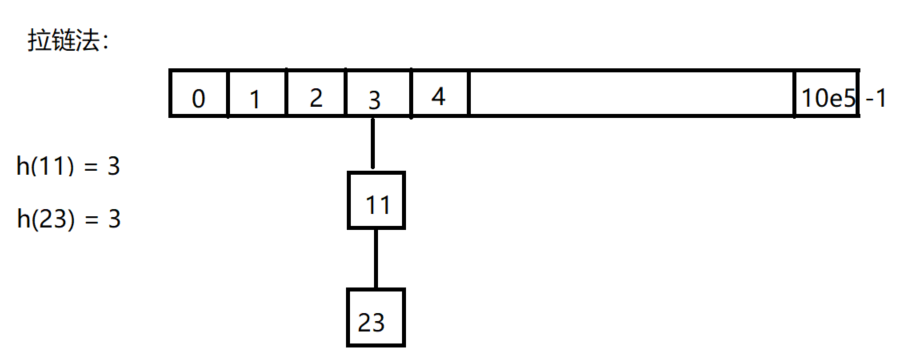
** 拉链法写法**

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


# include <iostream>
# include <cstring>

using namespace std;

const int N = 100003; // 大于100000的最小质数

int h[N], e[N], ne[N], idx;

void insert(int x)
{
	int k = (x % N + N) % N; // 目的是让hash值成为正数
	// 插入操作
	e[idx] = x, ne[idx] = h[k], h[k] = idx ++;
}

bool find(int x)
{
	int k = (x % N + N) % N; 
	for(int i = h[k]; i != -1, i = ne[i])
		if (e[i] == x)
			return ture;
	return false;
}

int main()
{
	int n;
	scanf("%d", &n);
	
	// 把所有的槽先清空(单链表-1表示空指针)
	memset(h, -1, sizeof(h)); 
	
	while(n --)
	{
		char op[2];
		int x;
		scanf("%s%d", op, &x)；
		
		if(*op == 'I') insert(x);
		else 
		{
			if(find(x)) puts("YES");
			else puts("NO");
		}
	}
}

文章目录

哈希表