并查集

并查集的作用

  1. 将两个集合合并。
  2. 询问两个元素是否在一个集合当中。

并查集可以在近乎O(1)的时间复杂度完成这个操作。

基本原理

每个集合用一颗树来表示。树根的编号就是整个集合的编号。每个几点存储它的父节，p[x]表示x的父节点。

基本原理

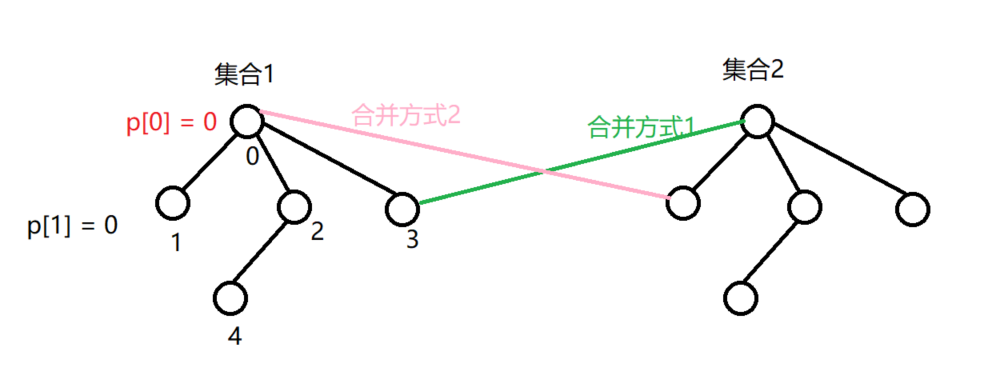
  1. 问题一：如何判断是否是树根： if(p == x)
  2. 问题二：如何求x的集合编号：while(p != x) x = p ;
  3. 问题三：如何合并两个集合：p 是 x 的集合编号，p[y]是y的集合编号。合并直接将p = y即可。

路径压缩优化

路径压缩优化

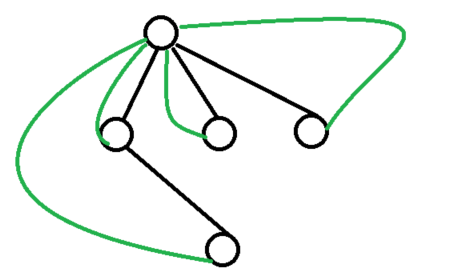
只是在第一次求根节点的时候会遍历一边，遍历一遍之后直接将当前节点指向根节点。

题目实例

合并集合

一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。

现在要进行 m 个操作，操作共有两种：

  1. M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
  2. Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

输入格式

第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤10e5

输入样例：

1
2
3
4
5
6

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

1
2
3

Yes
No
Yes

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include <iostream> 

using namespace std;

const int N = 100010;

int n, m;
int p[N];

int find(int x) // 返回x的祖宗节点 + 路径压缩优化
{
	if(p[x] != x)  p[x] = find(p[x]);
	return p[x];
}

int main()
{
	scanf("%d%d", &n, &m);
	
	for(int i = 1; i <= n; i++) p[i] = i;
	
	while(m -- )
	{
		char op[2];// scanf读字符串的时候可以自动忽略字符串和回车，scanf读一个字母建议使用字符串的形式
		int a, b;
		scanf("%s%d%d", op, &a, &b);
		
		if(op[0] == 'M') p[find(a)] = find[b];
		else
		{
			if(find(a) == find(b)) puts("YES");
		}
	}
	return 0;
}