堆

堆的作用

  1. 插入一个数 heap[ ++ size] = x; up(size);
  2. 求 集合当中的最小值。heap[1]
  3. 删除最小值。 heap[1] = heap[size]; size --; down(1);
  4. 删除任意一个元素。heap[k] = heap[size]; size --; down(k); up(k);
  5. 修改任意一个元素。heap[k] = x; down(k); up(k);

堆基本结构

完全二叉树。

完全二叉树

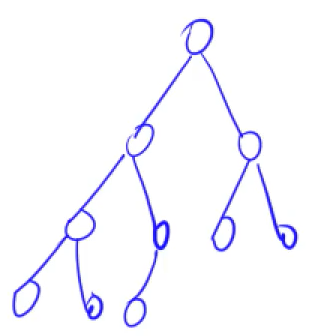
小根堆 每个点小于等于左右孩子，根节点为最小值。 大根堆 每个点大于等于左右孩子，根节点为最大值。

堆的存储

用一个一维数组来存储。

堆的存储

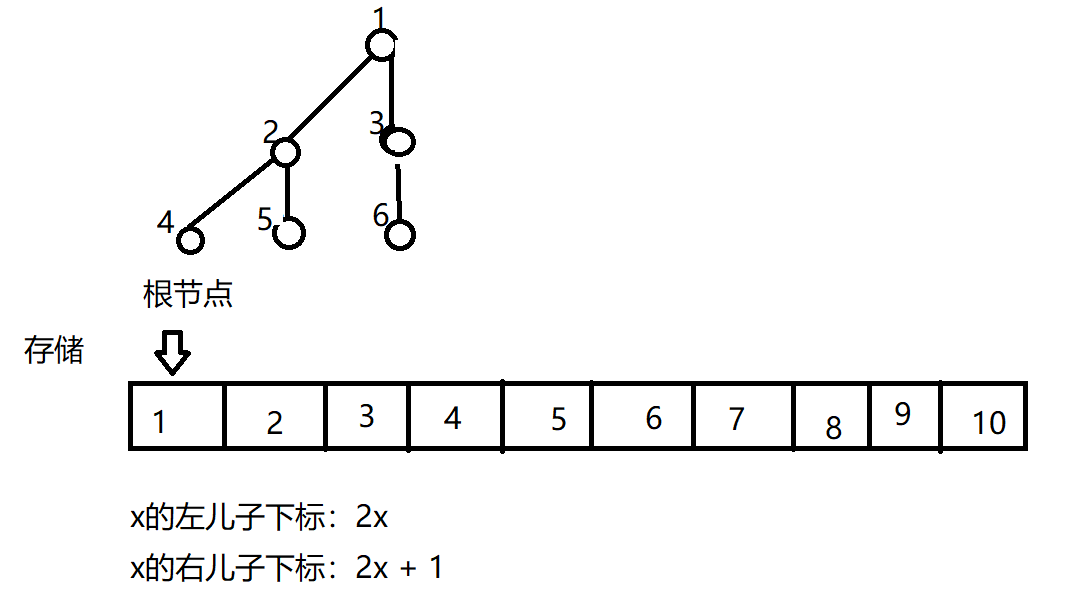
代码实现及示例

堆排序

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输入格式

第一行包含整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

输出格式

共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围

1≤m≤n≤10e5， 1≤数列中元素≤10e9

输入样例：

1
2

5 3
4 5 1 3 2

输出样例：

1

1 2 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], size;

void down(int u)
{
	int t = u;
	if (u * 2 <= size && h[u * 2] < h[t] ) t = u * 2;
	if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
	if (u != t) 
    {
    	swap(h[u], h[t]);
    	down(t);
    }
}

void up(int u)
{
	while(u / 2 && h[u / 2] > h[u])
	{
		swap(h[u / 2], h[u]);
		u /= 2;
	}
}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) scanf("%d",&h[i]);
	size = n;
	
	for(int i = n / 2; i; i --) down(i);
	
	while(m --)
	{
		printf("%d ", h[1]);
		h[1] = h[size];
		size --;
		down(1);	
	}
}